“DeepSeek許多重要創新出自實習生之手。”

這是前段時間社交網絡上盛傳的信息，不過這條信息並不誇張，因爲辛華劍就是在DeepSeek實習期間主導開發了專注於數學證明DeepSeek-Prover系列模型，他也是DeepSeek-Prover-V1.5論文的一作。

圖片來源：DeepSeek-Prover-V1.5論文

辛華劍本科畢業於中山大學邏輯學專業，現在是愛丁堡大學人工智能方向的一年級博士生，專注於大模型在數學定理證明中的創新應用。

去年8月發佈的DeepSeek-Prover-V1.5可以被看作是DeepSeek在數學證明領域的早期探索和技術積累，推動了大模型更好地解決形式化定理證明問題，當時被稱爲是“最強形式化推理模型”。

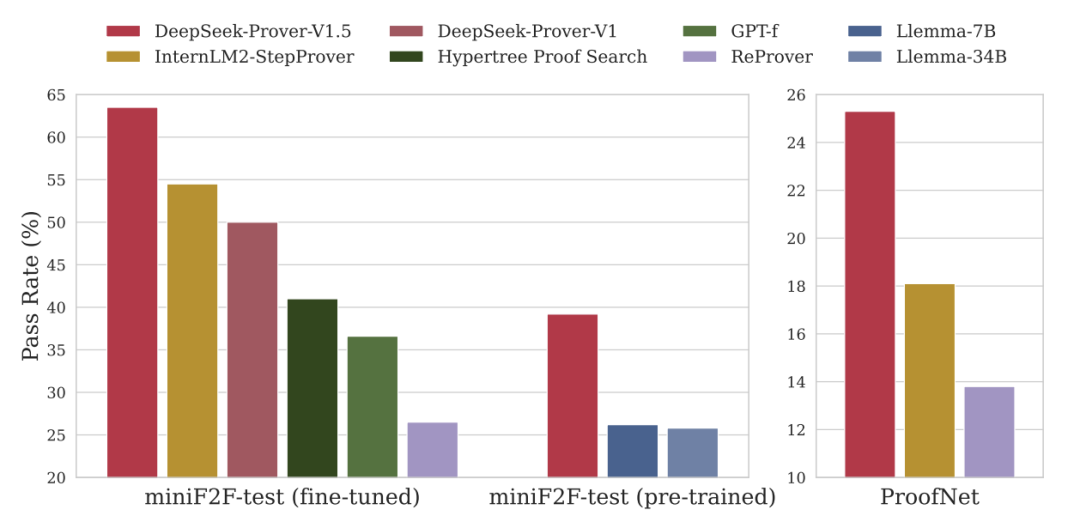
模型在Lean 4形式定理證明基準上的通過率：DeepSeek-Prover-V1.5在高中階段miniF2F-test基準（Zheng et al., 2022）和本科階段ProofNet基準（Azerbayev et al., 2023）上表現突出，圖片來源：DeepSeek-Prover-V1.5論文

在大模型中，非形式化推理是其理解和生成自然語言、進行常識推理的基礎，就像是人類平時聊天或思考問題時的自然方式；而形式化推理則賦予大模型在特定領域（如數學、代碼）進行精確、嚴謹推理的能力，它有嚴格的規則和格式，每一步推理都必須符合邏輯規則，不能隨意跳步或省略。

“DeepSeek-Prover在DeepSeek算是一個比較獨立的探索性項目，它的初衷是探索通過形式化系統更好地構造自然語言的嚴格推理數據。”辛華劍告訴“甲子光年”。

隨着AI推理能力的提升，使用AI來證明數學問題已經成爲一個重要的研究探索方向，形式化數學也成爲了討論熱點。

形式化數學是指使用嚴格的數學語言和邏輯系統來描述和推理數學概念、定理和證明的過程。著名數學家陶哲軒就認爲，形式化數學和AI的結合將使數學研究更加高效、協作和規模化。他樂觀地預測，未來數學家可以在AI的輔助下，一次性證明數百或數千條定理。

英國當地時間2月14日下午，在UKTI.HUB（英倫科創）舉辦的活動上，辛華劍發表了一場題爲《大語言模型時代的形式化數學革命》的演講並回答了“甲子光年”和現場觀衆的提問。倫敦大學學院（UCL）裏的一間教室，湧入了180多名觀衆。

“這個項目的理想是，最終能夠推出一種服務或產品，幫助數學家快速驗證一些比較簡單的猜想，把數學家從細節當中解放出來。”辛華劍說。

本文，“甲子光年”首家整理呈現辛華劍在本場活動的演講和問答環節。其中問答在文中最後一部分，辛華劍回答了DeepSeek算力利用率、MCTS對模型訓練意義、大模型幻覺、AI未來發展等問題。相關內容經編輯後有刪改。

1.形式化數學的歷史淵源

大家好，我是辛華劍。

今天我將和大家分享一些關於形式化數學的背景知識，以及探討如何利用大語言模型在數學推理中應用形式化方法，並展望其可能帶來的未來影響。

需要強調的是，接下來我所分享的內容，純屬個人觀點，不代表任何組織機構的立場。

首先，什麼是形式化數學？

或許對大家來說，這並不是一個非常熟悉的概念。簡單來說，形式化數學強調使用精確的符號語言來表達數學陳述和證明，其所有的定理及其證明都必須從一些確定的公理出發，並遵循明確的、可以被機器驗證的邏輯規則。

事實上，形式化數學並非一個全新的概念，它有着悠久的歷史。

早在萊布尼茨時期，他就提出了“普遍語法”的概念，希望人類所有的思想都可以通過計算來判斷真假。比如說當兩人發生爭執時，只要坐下來計算一下，就能得出誰對誰錯的結論。他希望用代數符號的方法來刻畫這種操作，這實際上可以看作是現代邏輯學的肇始。

時間來到希爾伯特時代，形式化數學作爲一項研究計劃已經基本成熟。在他的時代，我們如何進行形式化數學呢？首先，我們需要挑選公理系統，並驗證其一致性、相互獨立性和邏輯完備性。此外，還需要考慮一個關鍵問題：是否存在一種能行的方法，能夠在一個理論中判定一個問題的答案？雖然哥德爾、丘奇和圖靈的工作已經否定了這種可能性，但數學的機械化或自動化仍在不斷發展。

從20世紀30年代開始，布爾巴基學派強調使用公理化的方式來重構整個數學體系。他們認爲，人類數學家並非無所不能。當他們對某些數學文本的正確性產生質疑時，他們訴諸於將它們進行形式化的一種可能性，直到他們認爲這種可能性只是一種練習，不需要額外的思考，他們就會停止這樣形式化的過程。

這也就是說，形式化是他們保證數學正確性的一個根本策略。

進入計算機和人工智能時代，麥卡錫提出了使用計算機來書寫和檢查證明，他認爲這樣的證明可能會比數學家給出的更短。這是因爲許多具體細節可以由計算機來代替人類進行驗證，可以被很好地封裝起來，不暴露給數學家。數學家只需要關注證明的主要內容和數學思想，一些邊界條件之類的檢查，就可以完全交給計算機來處理。

2.當代數學的工程化挑戰

雖然形式化數學擁有好的歷史淵源，爲什麼它至今仍未被數學界廣泛採納？以及，爲什麼我們認爲它將引發一場革命？

我們認爲，當代數學面臨着一種工程化的挑戰。

我們觀察到，現代數學證明的篇幅已經變得極其龐大，動輒數百頁甚至上千頁。要掌握如此龐大的證明篇幅規模，並通過同行評審進行驗證，需要耗費巨大的人力成本。

舉個例子，即使人類專家花費數年時間共同驗證一個大型證明，仍然有可能出現錯誤。例如，四色定理的早期證明最初被接受，但後來卻被發現存在問題。

此外，知識管理也是一個關鍵問題。

隨着數學的不斷發展，無論是在學科分支的數量上，還是在每個學科的深度上，都已經遠遠超出了一個人類專家能夠掌握的範圍。

我們會說亨利·龐加萊是最後一位全才數學家，現在已經沒有人能夠掌握所有數學分支的最新進展。數學家之間在工作上呈現相對分散的狀態，這對於數學的可持續發展來說並不是一件好事。

一個典型的例子是，2003年，黑爾斯提出了關於開普勒猜想的一個長達300頁的證明。《數學年鑑》（Annals of Mathematics）組織的12人小組花了四年時間，也沒有對其正確性做出十足的判斷。最終，黑爾斯組織21個人的團隊花了12年時間，將這個龐大的數學證明利用Isabelle和HOL Light（證明助手軟件，能夠保證了證明之於“數學公理”與“邏輯規則”是正確的）上進行了形式化，才最終驗證了其正確性。

事實上，黑爾斯在他的原文中提出要做這件事的目的，並不僅僅是爲了打消這12人的疑慮。他認爲，對於數學的長期發展而言，形式化方法是一個根本的解決方案。

時間來到2024年，陶哲軒也正在推進關於形式化數學方向的研究。

有采訪者問陶哲軒：“爲什麼形式化數學使得數學家互相之間對工作結果的信任有了改變？”陶哲軒說，形式化數學最好的一個特性是，它能夠將一個大的問題分解成相互獨立的很多方面，大家只要根據自己所專長的方面來提交自己的證明代碼，而證明代碼的正確性驗證是由證明助手以計算機程序執行的方式來徹底完成的。也就是說，數學家不需要逐行檢查別人的證明是否真的完全正確，才願意相信他的工作成果。

因此，他認爲這種工作方式是一種更加可以擴展到大規模的數學工作方式。他在對PFR假設的證明進行形式化的項目中，與超過20人的團隊來協作完成，這已經比他通常合作的規模要大一些。他認爲，隨着大家對這套計算機輔助證明系統的瞭解，以及對這種形式化數學的工作方式的瞭解，實際上可以推廣到更大的規模。也就是說，我們可以像軟件工程大規模開發一樣來做數學，他認爲這是一種非常現代化的方式。

另一方面，愛丁堡大學信息學院的教授Alan Bundy總結道，隨着數學的規模越來越大，我們面臨一個二難推理：要麼我們必須放棄所有這種大定理，要麼我們必須訴諸於計算機的輔助來進行證明。

3.形式化數學作爲一種解決方案

那麼，形式化數學作爲一種解決方案，是怎樣被實現的？

這裏舉一些具體的例子。

現在流行的智能助手語言大概有四種，例如Coq、Lean、Isabelle和Mizar。

以Isabelle爲例，我們如何在Isabelle中進行形式化證明？一個非常具體的例子，也是在Wikipedia上提供的演示例子：如何證明√2不是一個有理數？

我們會發現，這個在Isabelle中進行的證明在思路上與人類的證明是一致的，它也利用反證法，也逐漸推出一些中間結論，並利用這些中間結論逐步推導出矛盾。

最關鍵的是，我們不僅僅要在一個定理的證明內部進行工作，我們實際上操作的是一個非常大的數學理論。這個龐大的理論涉及到非常多的定義、引理和定理，我們如何管理它們之間的相互關係？

陶哲軒在他的PFR項目中已經演示了Lean blueprints帶來的工作方式變化。其中，綠色的點是已經完成證明的部分，藍色的點是正在嘗試進行證明中的定理，白色的點表示還沒有被編寫的部分。而圖上的點之間的連線描述了這些定義和定理之間的依賴關係，也可以幫助更好地理解和分析整個項目。

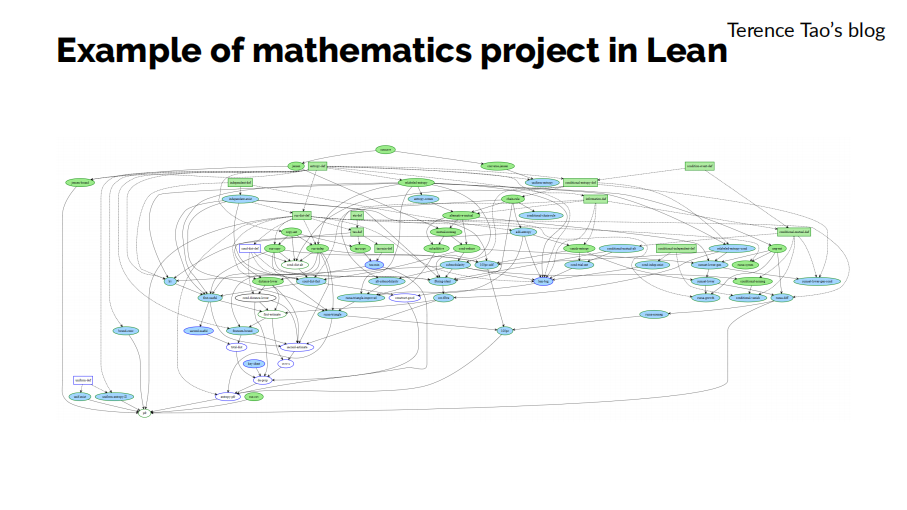
當這個blueprint中所有的點都變成了綠色的時候，我們就可以確鑿無疑地判斷這個整套數學理論已經完成證明了。

但是，爲什麼現在大家在學校裏仍然使用自然語言來學習和研究呢？這是因爲有很多的阻礙，使得我們還沒有采用形式化的方法。

一方面是文化上的阻礙。數學工作者仍然更習慣於使用紙筆來進行更靈活的推導，而形式化數學往往只被認爲是工程化的輔助技巧，而不是在數學思想上有啓發的技術。

另一方面，形式化數學的學習曲線非常陡峭。它有非常複雜的程序語法和語義，需要使用者同時瞭解數學思想、以類型論或集合論進行形式化的邏輯方法，以及編寫程序語言的技術。

結果就是，同樣一個證明，在形式化系統裏面做和用自然語言做相比，很多時候要多花十倍甚至二十倍的人工成本，這其中包括要額外證明很多在直觀上非常直接的、但嚴格證明非常瑣碎的引理。

其他的因素還包括，可能你在Mathematica裏面可以順利地算出一個很複雜的積分，但要使這樣的積分結果被Lean這樣的嚴格證明系統接受，目前仍然缺乏自動化的銜接機制。

4.大語言模型在形式化數學的應用

接下來，我想和大家探討一下大語言模型（LLM）在形式化數學領域的發展。我將從以下幾個方面展開：

目前 AI 發展到了什麼階段？

如何將 LLM 應用到形式化數學中去？

LLM 在形式化數學領域未來的發展方向是什麼？

面臨的挑戰和侷限有哪些？

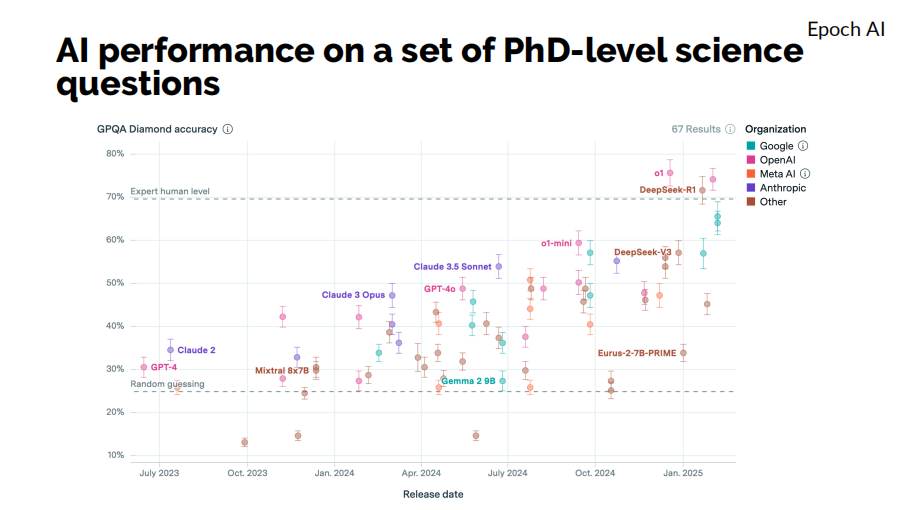
首先，我們可以考慮GPQA Diamond，這是一個衡量PhD水平科學問題的榜單。我們可以看到，從2023年到2025年，大語言模型在解決這些問題上的能力有了顯著提升。特別是OpenAI的o1、o3和DeepSeek-R1等模型，其水平已經略高於人類專家的水平。

這意味着，我們距離實現通用人工智能（AGI）可能已經並沒有想象中那麼遙遠。

另外，OpenAI 前不久發佈的一份報告顯示，目前最先進的大語言模型在算法競賽上的表現也十分驚豔。在codeforces編程競賽平臺上，o1模型最高能達到98%甚至更高的分位數，這意味着它已經位於前2%的水平。在2024年國際奧林匹克數學競賽（IOI）上，他們的模型能達到362分，這已經達到了人類金牌選手的水平。

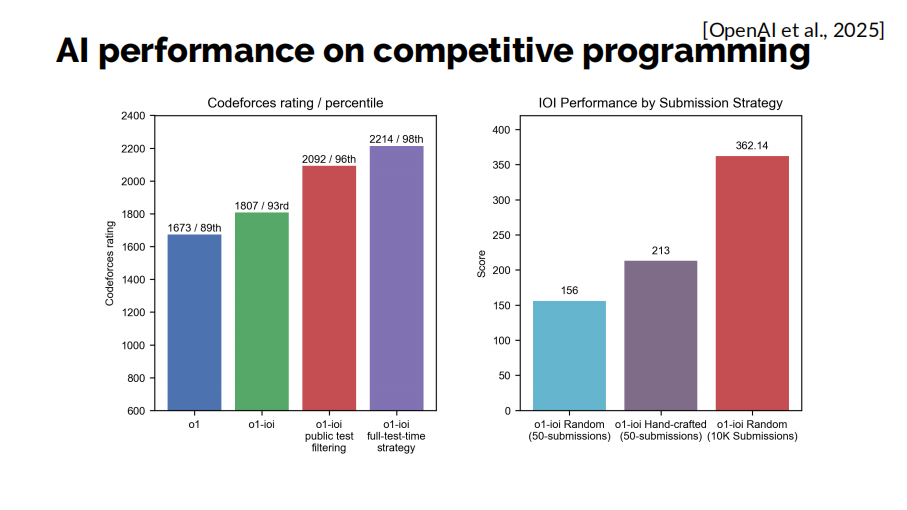
在數學方面，DeepMind去年7月份發佈的形式化數學定理證明模型AlphaProof也取得了重要進展。和我們的做法一樣，該模型也不是在自然語言上進行訓練和測試，而是在形式化證明系統Lean中進行的。它與專注幾何的模型AlphaGeometry2一道，在2024年的國際數學奧林匹克競賽（IMO）中獲得了28分的成績，距離金牌水平僅差1分。

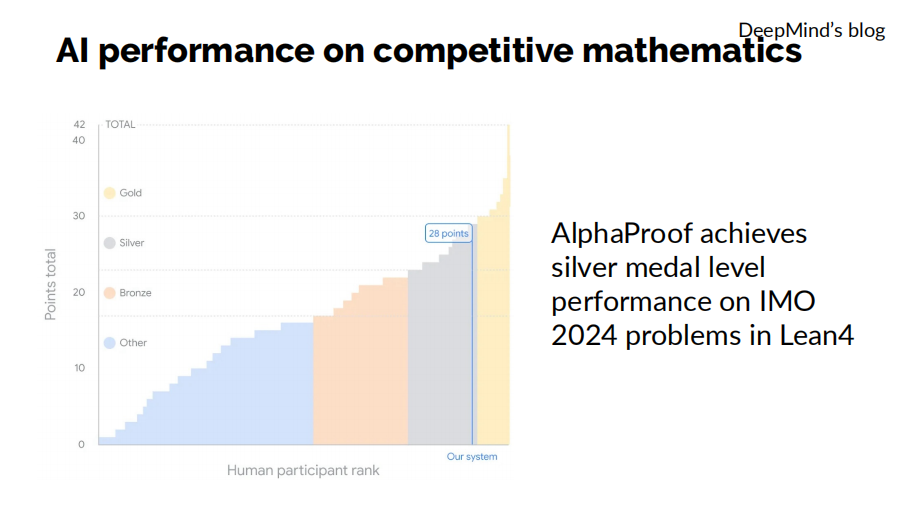
那麼，這些看起來像是奇蹟的模型是如何訓練出來的呢？其背後的訓練機制是怎樣的呢？

以AlphaProof爲例，它的訓練流程大致分爲兩部分。第一部分先收集 100 萬道人類數學問題，這些問題以自然語言描述，再使用神經網絡將其翻譯成一億道形式化數學問題。

然後，我們在此基礎上訓練解題神經網絡。該網絡採用了類似於AlphaGo的強化學習方法，不斷地嘗試對數學題目搜索證明，成功通過形式化驗證的證明拿來進行訓練，以此不斷迭代，不斷提升解題神經網絡的性能。

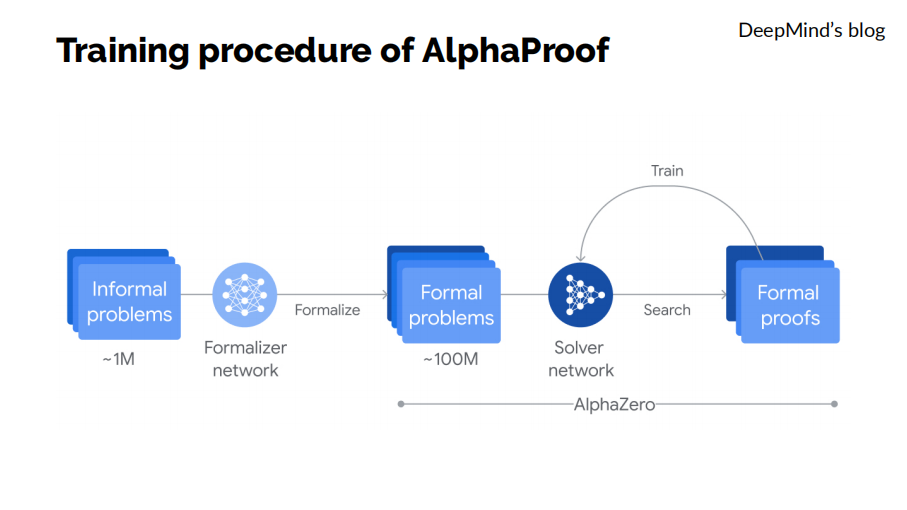
事實上，在2024年5月，我們的DeepSeek-Prover團隊就已經提出了一個相似的方法：我們同樣通過大規模的自動形式化方法來合成證明數據，進行迭代訓練，不斷提升定理證明模型的表現。

在我們的論文中，還分享了一些數據合成流程設計的細節。例如，使用模型生成的形式化數學問題可能是錯誤的，我們就讓模型同時嘗試證明它和證僞它。類似於AlphaGo在圍棋中進行“左右互搏”的方法，只要有一方面的證明成功，我們就認爲模型成功證明了該定理，並把該證明加入訓練數據中繼續進行迭代。

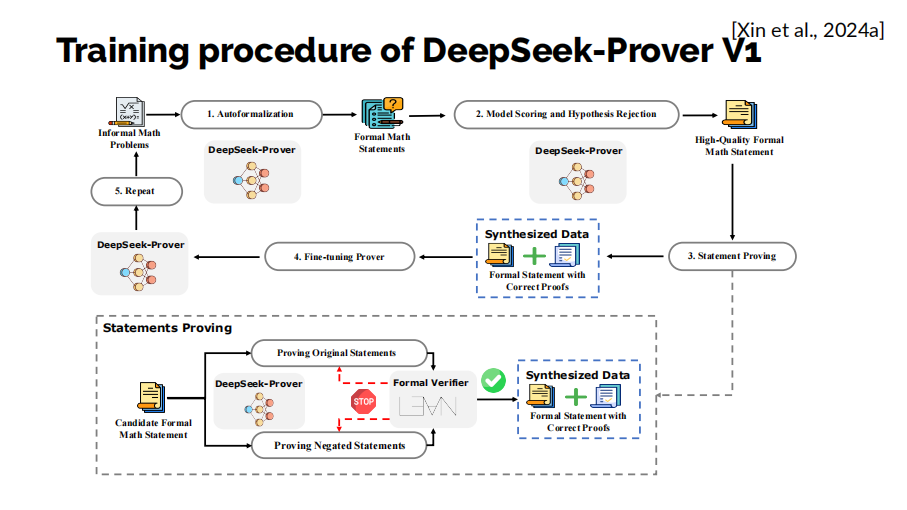
MiniF2F是一個標準的形式化定理證明Benchmark，主要衡量模型在高中數學競賽中的表現。2024年5月，我們的DeepSeek-Prover V1模型打破了Meta維持了兩年的SOTA（最先進水平）。此後，該領域變得越來越活躍，各種方法層出不窮，形式化定理證明模型也以更快的速度發展。

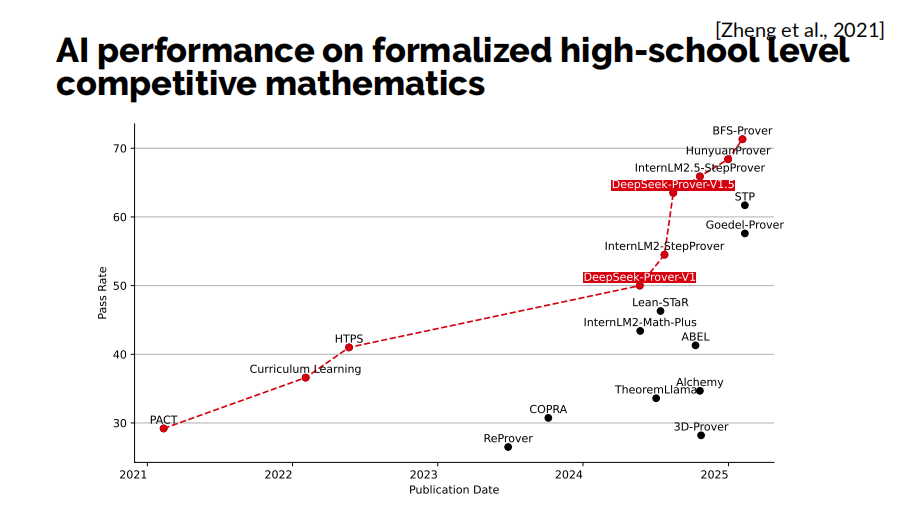
值得一提的是，在我們於2024年8月推出的DeepSeek-Prover-V1.5中，已經訓練得到了一些與目前流行的推理模型相似的行爲模式：大模型先進行一系列的思維步驟，然後再將這些思維步驟轉落實爲正式的回答。

正如以下實例展示的那樣，模型首先在註釋塊中進行完整的推理再開始進行形式化編碼，甚至在正式代碼的寫作中，對每一行證明的寫作前都先進行思考和規劃。這表明，我們的模型在一定程度上已經具備了先思考再作答的能力。儘管它在反思和回溯能力上仍然與目前最先進的推理模型有距離，但我相信這或許將是形式化數學定理證明模型的下一個突破的方向。

通過這個例子，我希望表達的是：形式化數學作爲大語言模型的一個應用領域或一種實踐方向，爲探索模型推理能力的訓練提供了嚴格驗證反饋的良好環境，能夠在一定程度上對其他更通用領域的研究起到借鑑作用。

接下來，我想談談對未來發展方向的展望。在形式化數學定理證明的領域，我們期望使用大語言模型在哪些方面取得進一步的突破？

首先，我們希望語言模型能夠主動提出一些有意義的數學猜想，證明它們可以幫助我們更好地完成目標定理的證明，或者發現已有數學結論之間的深層聯繫，甚至指導未來的數學研究方向。

更進一步，我們希望模型能夠獨立的發現一些數學抽象。

事實上，數學研究中最好的工作是能夠發現一些獨創的結構，而往往不僅僅是解決已經提出的猜想，也就是我們所熟悉的一句話就叫“提出問題比發現問題更重要”。

比如巴拿赫就說過，好的數學家就是發現定理之間、定理的證明之間的相似性，而最好的數學家能夠發現類比之間的類比，或者說發現更加高階的抽象。

這方面的工作其實也已經有探索，比如說在2021年時候有一個叫DreamCoder的項目，已經在相對簡單的Lambda Calculus上取得了進展。它從一些非常簡單的概念出發，能夠成功抽象得到複雜的概念，甚至發現了一些物理定律。

最後， 我們希望語言模型能夠獨立地構建一個完整的數學知識庫。

例如，人類在數學工作中、甚至是模型在迭代訓練中都會發現很多零散的定義和結論，它們之間存在重疊或依賴關係。我們希望語言模型能夠以一種結構化的方式將它們整合起來，形成一個層次分明、結構良好的知識體系，在其中更一般的定理可以統攝更具體的定理，實現從高層觀點到初等事實之間的整合。

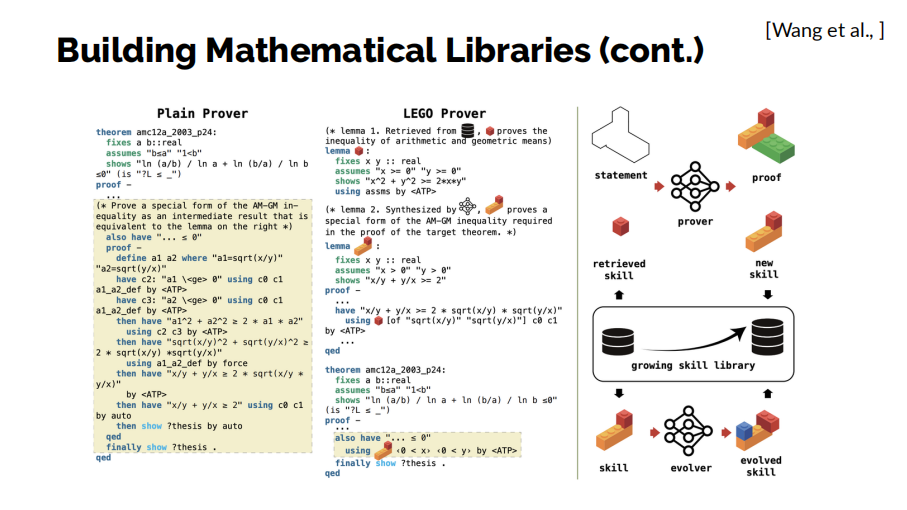
實際上，我們在2024年也已經有一個非常相似的工作，LEGO Prover，它獲得了2024年頂級學術會議ICLR的口頭報告推薦。和以往的的模型嘗試直接生成完整證明不同，我們讓模型在嘗試證明之前先提出一些引理，利用這些引理能夠幫助我們更好地證明目標定理。在這個過程中得到的這些引理會被收集到技能庫中以供稍後複用，以這種方式我們能夠引導模型積累知識、提升性能。模型手上的工具越來越多，可以更好地來適應由弱到強的泛化，一步一步地學會做一些更加複雜的問題。

5.LLM在形式化數學中的挑戰和侷限

最後想要分享一下在形式化數學定理證明領域應用大語言模型仍然存在的一些挑戰和侷限。

首先，數據稀缺。大語言模型的訓練是超大規模數據驅動的，但形式化數學領域的數據相對稀缺。這使得直接訓練模型變得非常困難。因此，這個領域的發展會更加依賴合成數據的作用。

其次，自然語言與形式語言的翻譯。正如我們之前談到，自然語言和形式語言之間的相互翻譯並非易事。

第三，形式系統的複雜性。形式系統爲了保證嚴格推理，每個定理都必須在原則上能夠追溯到原始公理，這會導致整個系統變得非常臃腫龐大。例如Lean的標準數學庫中有超過2000個代碼文件、將近180萬行代碼，進行新的定理證明需要準確調用其中已有的結論，這實際上是一個非常困難的任務。我認爲要使用大語言模型做好形式化數學需要擁有在大規模代碼庫上工作的Agent能力，而這目前是一個公認的挑戰。

那麼，如果我們在數學領域成功應用了大型語言模型，又意味着什麼呢？

我會從對數學研究、對工業規模的驗證、對數學教育、對一般應用這四個方面去談。從我個人的觀點看，DeepSeek之所以受到這麼大的關注，很大程度上是因爲它展示了一個道理：如果說智能可以就像自來水一樣，價格低廉、規模可擴展、質量可以信賴，它是會改變整個世界的。這就像古羅馬能夠創造一種繁榮的文明形態，與輸水管道等可靠的基礎設施是密不可分的。

對於數學研究而言，我們希望能開發一種服務或產品，幫助數學家快速驗證一些簡單的但勞動密集的猜想，將他們從繁瑣的細節中解放出來。語言模型可以充當人機交互的接口，將自然語言問題翻譯成代碼，利用已有知識庫中進行嚴格驗證，並將結果以自然語言的形式反饋給數學家。

第二個方面就是關於工業中的大規模驗證。事實上，除了數學之外，形式化方法也在軟硬件驗證上有廣闊的應用，例如英特爾在芯片驗證上廣泛使用了大規模的SAT/SMT求解器，而定理證明器可以在更高層次的抽象上完成嚴格的規約驗證。然而，由於需要專家花費長時間進行證明編碼，在實踐中廣泛實施中的代價非常高昂，極大限制了形式化方法的應用。我們希望語言模型能夠加速形式驗證的普及，使其能夠以更低廉、更可擴展的方式應用於更廣泛的領域，避免軟硬件漏洞可能導致的巨大損失。

第三個方面就是教育。我們可以保存和傳承那些可能被遺忘的數學知識。隨着老一代數學家的退出，他們的研究成果可能會逐漸被人遺忘。但語言模型可以成爲一種可擴展的知識載體，保存和傳承這些長尾的數學知識。

最後，對於一般的應用來說，實際上數學並不只是數學家關心的問題，在生活、工作中有很多事情可以用數學的辦法解決。一個例子是運籌優化，目前的解決方案也因爲專家人工成本過高而無法惠及所有需求，但大語言模型可以大大降低成本、擴展適用的規模。另一個例子是算法開發，構想一個算法往往是比較快速的，但是我們如何能夠判斷這個算法的效率？這實際上是一個比較複雜的數學問題。如果說我們有一個非常好的數學大語言模型，能夠幫我們快速運用數學工具估計一些複雜算法的複雜度的話，那這對算法的演進也是一件好事。

總之，大語言模型爲數學提供了一種嚴格且可持續的知識載體和應用手段，我們認爲它在自動化形式化和定理證明方面具有廣闊的應用前景。

雖然目前仍然面臨數據稀缺、自然語言對齊以及系統複雜性等挑戰，但我們相信，隨着技術的不斷發展，大語言模型將在數學領域發揮越來越重要的作用，同時也將推動軟硬件驗證以及其他科學應用的進步。

6.問答環節

問：DeepSeek有哪些創新之處？這些創新對AI開發者有哪些啓示？在提升算力利用率方面，我們應該關注什麼呢？

辛華劍：DeepSeek震動華爾街一個方面是它的訓練成本非常低，這與DeepSeek在算力管控方面的工作密不可分。在實際工作中，尤其對於大模型而言，如何制定合適的算力策略至關重要。如果我們有更多的卡，肯定不會太顧及算力的使用效率，所以有些時候資源有限是能夠促進創新的活躍的，但另一方面，在算力不足的情況下，也難以在scaling law上獲得正確的認知。這其實是一個比較矛盾的問題。

問：DeepSeek-Prover-1.5的定理證明在邏輯上是百分之百正確的嗎？

辛華劍：我們強調通過驗證的證明是正確的，但這句話的前提在於我們對數學問題進行的形式化建模是正確的，以及它所最終實現的這個程序語義是符合我們期望的。

問：MCTS（蒙特卡洛樹搜索）對於模型訓練很重要嗎？

辛華劍：我們在DeepSeek-Prover-V1.5階段確實做了MCTS，但我們發現MCTS和獨立的採樣相比，表現並沒有非常大的收益。這可能與DeepSeek-R1技術報告裏說MCTS不太成功的結論是吻合的，不過在做R1的時候我已經離開DeepSeek了，所以我也只是猜測。

問：在資源有限的情況下，如何分配訓練和推理資源才能達到最佳效果？“大模型+無推理”和“中模型+花費更多token來做推理”哪個更好？

辛華劍：這是一個非常好的問題，也是我們在做Prover項目中實際面臨的挑戰。比如，在初期探索階段，我們是用小規模模型（如幾百M）進行大規模的MCTS（蒙特卡洛樹搜索），還是用更大規模的模型（如幾十B）來做小規模的推理？一個可以參考的例子是，去年在AIMO（人工智能數學奧林匹克競賽）的第二名團隊對模型採樣方法以及規模上的平衡做了細緻的研究，大家參考他們的報告《An Empirical Analysis of Compute-Optimal Inference for Problem-Solving with Language Models》。

問：AI是否會取代人類從事科研工作？例如，在數學、物理、化學等領域，哪些學科更容易被AI賦能？

辛華劍：我個人從事AI For Math的研究，我認爲數學是一個AI與人類進行溝通的良好橋樑。因爲數學是一個更傾向於純粹的思辨，而非實驗的學科。這使得在AI大模型開發階段，與環境交互的方式更加簡潔，從而方便AI算法的開發和驗證。當然，最近我們也看到AI在實驗科學領域也有所應用。例如，有研究機構嘗試讓AI參與實驗，甚至讓AI像學生一樣手動進行實驗，從中獲取經驗和知識。我認爲，AI在各個科研領域都在進行探索，而未來2到5年可能會有更顯著的進展。

問：LLM的幻覺問題會對數學定理造成怎樣的影響？

辛華劍：這個問題非常困擾我們。我們發現很多時候它會提出一些數學庫裏面根本就沒有的定義或定理，或者說它在訓練過程中記住了一些名字，但這些名字在當前的使用階段已經不再使用了，但模型仍然會使用類似的東西。我覺得這方面的解決歸根結底需要Agent能力，需要大語言模型和整個系統進行充分的交互，實際判斷它現在工作的這個基礎數學庫到底已經有什麼樣的內容。

問：展望未來十年，人工智能領域最令人興奮的機會是什麼？最大的挑戰又是什麼呢？

辛華劍：事實上，在o1出現之前，我根本沒有想到可以把思維鏈拉得這樣長，出現足夠自主反思能力的推理模型。我認爲這樣的技術進展，往往非常跨越性的，即使是在一線訓練模型的同學也不一定能對未來有準確的預測。我感覺很多時候AI就像一種魔法，它會有怎樣的結果，只有真正動手試一試才知道。對於我們來說這恰恰是做AI研究工作最大的motivation（驅動力），它確實是一個需要充分想象力的學科。