編輯：Aeneas KingHZ

【新智元導讀】AI輔助人類，完成了首個非平凡研究數學證明，破解了50年未解的數學難題！在南大校友的研究中，這個難題中q=3的情況，由o3-mini-high給出了精確解。

就在剛剛，AI完成了首個非平凡研究數學證明！

完成這項研究的，是美國紐約布魯克海文國家實驗室凝聚態物理與材料科學分部的一位華人學者Weiguo Yin。

在這項研究中，作者在一維J_1-J_2 q態Potts模型，通過引入最大對稱子空間（MSS）方法，對其精確求解。

具體來說，作者將q^2×q^2的傳遞矩陣進行塊對角化。

而q=3的情況，正是基於OpenAI的最新推理模型o3-mini-high來精確求解的。

在AI的幫助下，研究者成功證明，模型可以映射爲一維q態Potts模型，其中J_2作爲最近鄰相互作用，J_1則作爲有效的磁場，這一結果擴展了之前在q=2，即Ising模型的證明。

注意，這個問題，在數學界有50年沒有解決。

論文引用了關於J_1−J_2伊辛模型（即q=2的Potts模型）的工作，這些工作可以追溯到1969年和1970年。

而o3-mini-high幫忙完成的這項證明，爲衆多懸而未決的物理問題（層狀材料中原子或電子順序堆疊的問題，以及非常規超導體中常見的T_c-拱形相的形成等），提供了全新的見解。

AI模型在科學研究中的巨大潛力，也再一次被證實！

Weiguo於2004年加入布魯克海文國家實驗室擔任研究員，並於2006年晉升爲助理物理學家，2008年晉升爲副物理學家，2011年晉升爲物理學家。

他的專長在於結合第一性原理、有效哈密頓量和機器學習方法，研究強關聯體系、挫敗磁性、超導性、多鐵性、混合的3d-5d化合物、拓撲材料和非平衡態。

1998年，他獲得南京大學的博士學位，並榮獲2000年國家優秀博士學位論文獎。

五十年未解的數學難題，被AI解決了

在凝聚態物理、材料科學、量子信息學和微電子學等研究領域中，發現新的相和相變是一個核心挑戰。

挫敗磁體中存在許多不尋常的相，這些磁體通常用伊辛模型（Ising model）或量子海森堡模型（quantum Heisenberg model）來描述。

統計力學的第三個基本模型是q狀態Potts模型。

它是伊辛模型（q=2）的推廣，可以作爲研究從離散（伊辛）對稱性到連續（海森堡）對稱性轉變的有效中介。

特別是，一維J_1-J_2 Potts模型可能與衆多問題相關，這些問題涵蓋了從層狀材料中原子或電子有序的面外堆疊，如1T-TaS_2 中的“大衛之星”電荷密度波，到每個時間步都有多種選擇的時間序列問題，如乒乓球訓練設計。

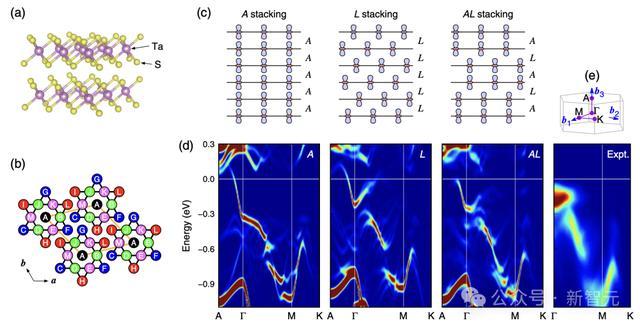
1T-TaS2中的“大衛之星”電荷密度波相關論文插圖

一維J_1-J_2 Potts模型

儘管一維和二維的J_1-J_2伊辛模型和海森堡模型已被廣泛研究，但只有一維J_1-J_2伊辛模型通過轉移矩陣法得到了精確解。

對於一維J_1-J_2 Potts模型，至今仍沒有精確的解析解。

因爲當q=3時，該模型已經展現出與q=2（即伊辛模型）不同的基態相行爲（見下圖），因此精確求解任意q的模型具有基礎性的重要性。

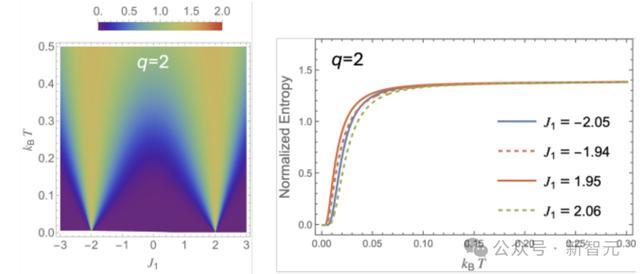
伊辛模型：不同的基態相行爲

挑戰在於轉移矩陣的階數迅速增加，階數爲q^2。

可想而知，q=3時的9×9矩陣已經很難進行解析求解，而q=10^10時的10^10×10^10矩陣，即使是數值計算也無能爲力。

先前的研究將任務轉化爲數值計算有效的q×q矩陣，採用整數q形式的轉移矩陣法，或連續q形式的轉移矩陣。

儘管物理學的透明度較低，但仍然無法得到精確的解析結果。

因此，對於一維J_1-J_2 Potts模型，至今仍然缺乏其中豐富相行爲的直觀理解。

OpenAI o3-mini的創舉：非平凡證明

最近的兩個發展爲這一長期未解問題提供了新的視角。

第一個發展是通過基於對稱性的塊對角化，將裝飾伊辛梯形的4×4轉移矩陣簡化爲有效的2×2矩陣。

這些發現爲一維挫敗Potts模型找到精確解，可能成爲這一重要新方向的里程碑。

第二個發展是OpenAI最新的推理模型o3-mini-high，推導出了一個優雅的方程，在外部磁場下，可以確定裝飾伊辛模型中UNPC的臨界溫度。

因此，作者受到啓發，逐步提示AI推理模型，去處理整數q形式的轉移矩陣。

儘管AI的回答中有不少錯誤，針對q=3的情況，最終找到了一種基於對稱性的塊對角化方法，可以將一維J_1-J_2三狀態Potts模型的9×9轉移矩陣解析地簡化爲有效的2×2矩陣。

對於一般的q，關鍵的對稱性是q個Potts狀態的全排列對稱性。

換句話說，哈密頓量（因此在整數q形式中的轉移矩陣）在任何對標籤{1,2,3,...,q}的排列下都是不變的；它的對稱羣是Sq。

雖然AI未能進一步推進，但警告說隨着q的增大，排列的數量急劇增加。

然而，q=2和q=3的精確結果，特別是兩者都歸結爲2×2矩陣，啓發了作者：

由於在熱力學極限下只有轉移矩陣的最大特徵值（λ）才重要，因此任務簡化爲識別包含λ的對稱分離子空間。

隨後，作者發現這個子空間由兩個最大對稱向量張成，因爲所有轉移矩陣元素都是正的，這使得最終得到了一個解析的2×2矩陣。

因此，任意q的一維J_1-J_2 Potts模型的精確解，就這樣被找到了，而且過程出奇的簡單！

o3-mini-high具體起了什麼作用

下面我們就來看看，o3-mini-high是如何在這項研究中推導出關鍵方程，對q=3的情況精確求解，從而確定了裝飾伊辛模型中UNPC的臨界溫度的。

首先，o3-mini-high證明，根據其知識，1D J_1-J_2 Potts模型尚未被精確求解。

接着，模型被提示使用1D J_1-J_2三態Potts模型的之字形梯形版本。

在這種情況下，AI正確地給出了以下哈密頓量表達式：

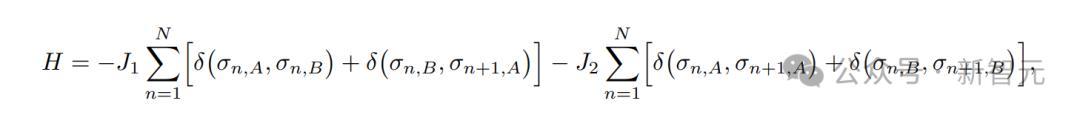
隨後，AI正確地生成了以下傳遞矩陣的表達式。

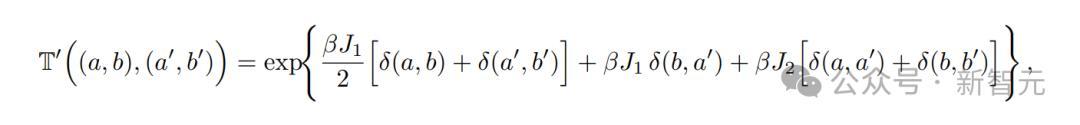
其中，(a, b)是由一對自旋組成的“梯級”狀態，(a', b')是鄰近梯級狀態。

假設一組梯級狀態按以下順序排列：(1, 1), (1, 2), (1, 3), (2, 1), (2, 2), (2, 3), (3, 1), (3, 2), (3, 3)。

若使用簡寫符號，則傳遞矩陣可以明確地表達爲如下形式。

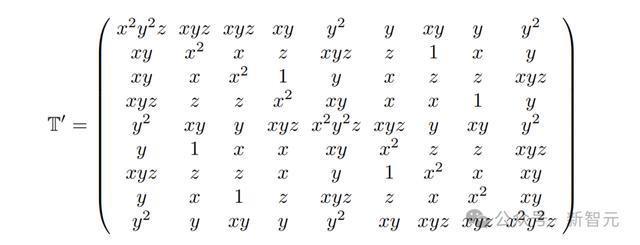
對於上面這個T'矩陣，AI被提示說，一定要確保

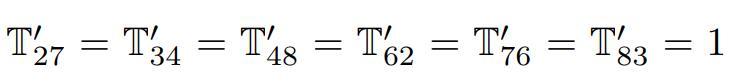
，從而糾正它的錯誤，並且識別出S_3的對稱羣。

然後，AI被提示將T'進行塊對角化。

它發現，T'可以通過變換下列這個矩陣來進行塊對角化，從而得到

。

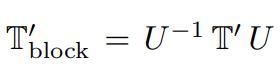
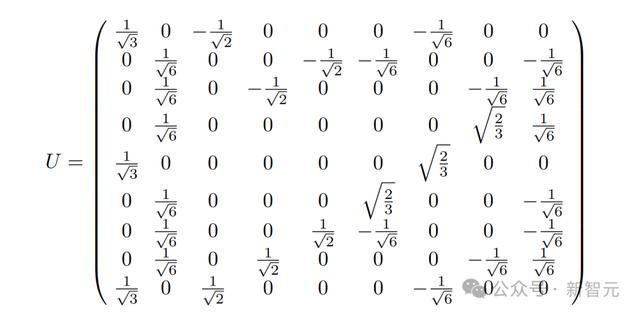
因此，得到的塊對角化傳遞矩陣的前2×2塊由

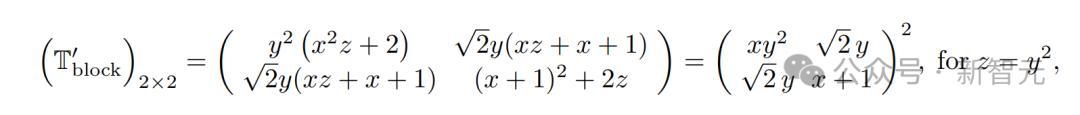
給出，其較大的特徵值是λ，即傳遞矩陣T'的最大特徵值。

最後，AI被提示生成上述對話的原生Wolfram Mathematica 14.2代碼。

這個任務在幾秒鐘內就完成了，幾乎不需要修正。

然而，AI卻未能生成適用於一般q的可用Mathematica代碼。

相反，它警告說，隨着q的增加，S_q對稱羣中的排列數會急劇增加。

當被進一步要求時，AI創建了一些假Mathematica函數，並表示“這些函數可能值得實現”。

五十年數學難題的精確解

考慮以下哈密頓量[圖1（a）]：

爲了構建轉移矩陣，研究者使用了重疊對的形式化方法來處理方程（1），每個單位格有一個自旋，得到轉移矩陣T。

同時使用該模型的等效鋸齒梯形表示，其中每個單位格有兩個自旋來獲得T′。

而且要滿足T′=T^2。

在熱力學極限N→∞時，配分函數爲

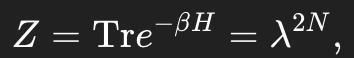
其中λ是轉移矩陣T的最大特徵值。

每個自旋的自由能由下式給出：

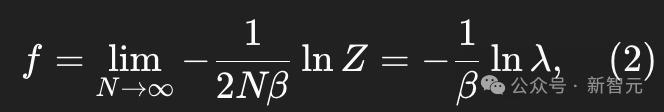
其中，β=1/(k_BT)，T是絕對溫度，k_B是玻爾茲曼常數。

由此得到的變換矩陣是一個q^2×2矩陣，它將q^2×q轉移矩陣T投影到與其餘部分解耦的2×2塊矩陣T_2，並且該矩陣由於不同的對稱性，得到如下方程4：

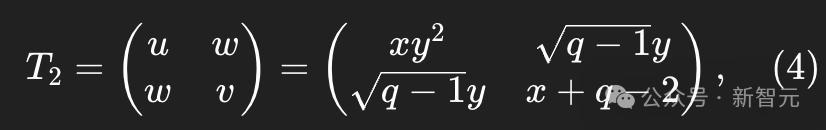
需要注意的是，最大對稱子空間意味着u、v和w的表達式可以通過組合分析直接得到。

轉移矩陣T的最大特徵值是T_2的較大特徵值，爲

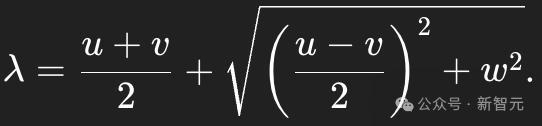
方程（4）的簡潔性爲理解一維J_1-J_2 Potts模型中的豐富相行爲提供了直觀的視角。

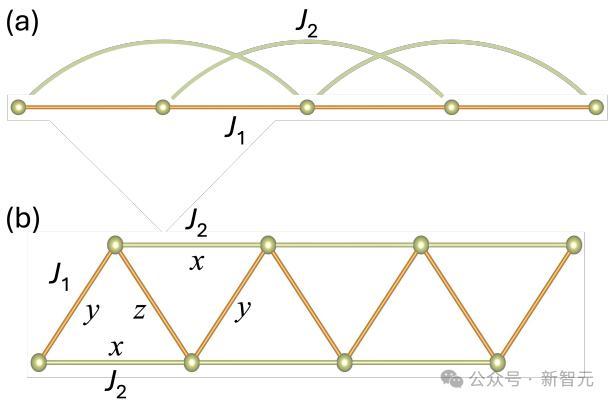
圖1:（a）單鏈J_1−J_2 Potts模型的示意圖和（b）其等效的鋸齒梯形表示。圖中的小球代表具有q個狀態的自旋。橙色的鍵表示最近鄰相互作用J_1，綠色的鍵表示次近鄰相互作用J_2

Potts模型的歷史性進展

爲了深入理解這些豐富的相圖，首先分析基態的相行爲。

在T=0時，對於所有q值，一維J_1-J_2 Potts模型有三個相，這些相由兩個臨界點（CPs）分開，這些臨界點由方程（4）中u、w、v的相對大小決定。

對於q=2（即伊辛模型），與q≥3情況有兩個方面的不同：

（1）q=2的兩個臨界點是對稱相關的，位於J_1=±2，而對於q≥3，它們位於J_1=0和J_1=2。

（2）對於q=2，三個相沒有宏觀的簡併性，而對於q≥3，存在一個或兩個具有殘餘熵的非平凡狀態。

圖3總結了左側和中間相以及兩個臨界點（CPs）殘餘熵的q依賴關係。

對於小的q，臨界點的殘餘熵（虛線）明顯大於相鄰相的殘餘熵（實線）。

因此，每個臨界點在J_1−T相圖中隨着溫度升高發展出V形區域（圖2左，q=2,3,4）。

兩個臨界點的V形區域匯聚在一起，形成一個類似T_c圓頂的區域，代表q≥3的中間隨機二聚化相。

當系統靠近臨界點時，它並不遵循常規的現象——即轉變到具有更高宏觀簡併性的相，而是轉變到臨界點發展的V形區域，這也在熵的T曲線中表現爲平坦區域（圖2右q=2,3,4），此時熵值等於對應臨界點的殘餘熵。

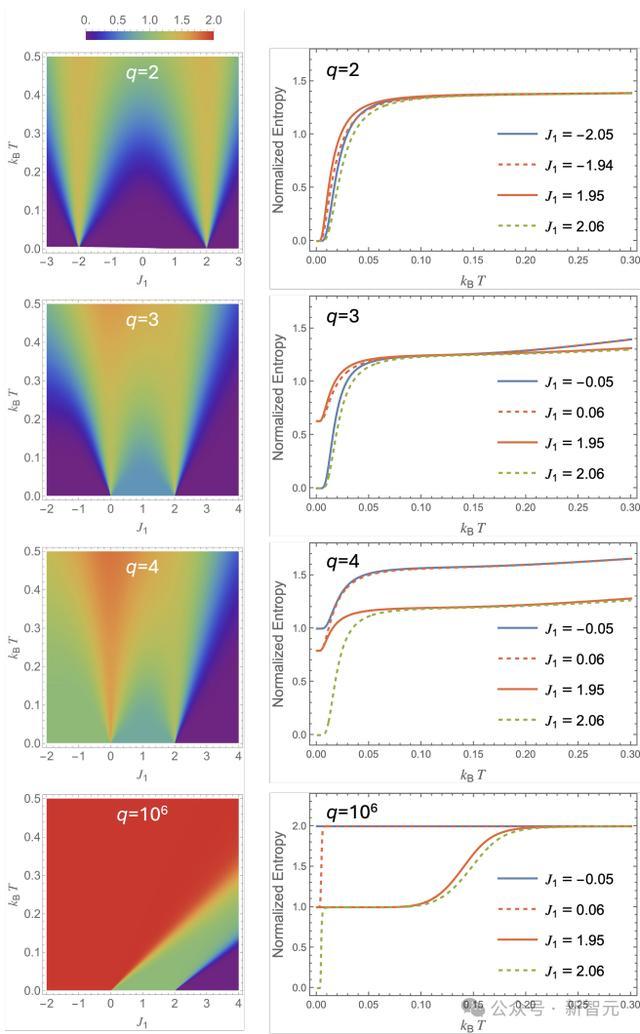
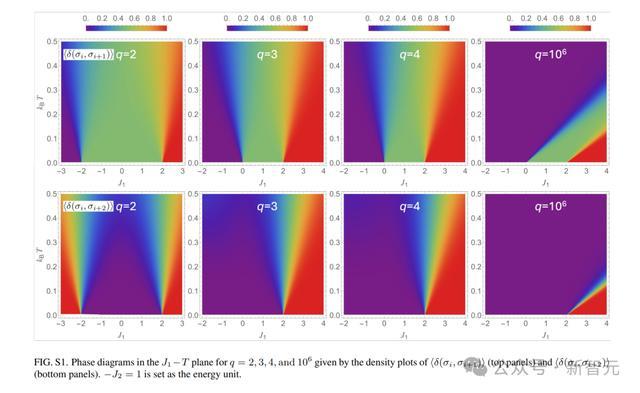
圖2：q=2,3,4和10^6的相圖

圖2左：在J_1−T平面上，歸一化熵2S(J_1,T)/ln(q)的密度圖。

圖2右：在臨界點附近，選定J_1值的2S(J_1,T)/ln(q)的溫度依賴性。−J_2=1被設定爲能量單位。

另一方面，圖3顯示，對於大的q，臨界點的殘餘熵（虛線）趨近於其相鄰相的殘餘熵（實線），最終變得無法區分——不再有V形的臨界點區域（圖2左，q=10^6）。

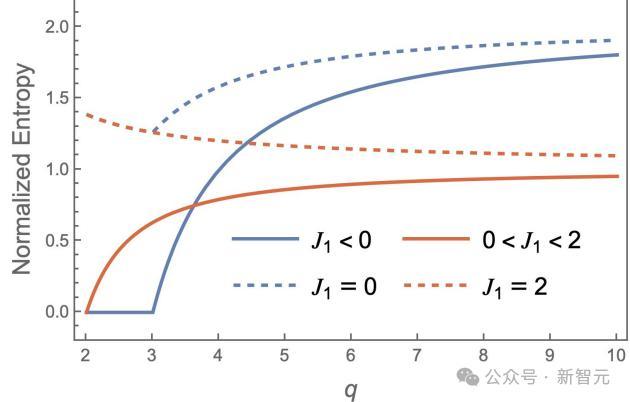
圖3：對於q≥3，在J_1的四個不同區域下，零溫度歸一化熵2S(J_1,0)/ln⁡q的依賴關係

當系統靠近相邊界時，它似乎遵循常規的現象，即轉變到具有更高宏觀簡併性的相。

特別是，當J_1>2時，低溫鐵磁相將經歷一個兩步的相交叉：首先轉變到中間的隨機二聚化相，然後轉變到左側的順磁相。

Tc圓頂是非常規超導性（如銅氧化物、鐵基超導體、扭曲雙層石墨烯等）中的一個關鍵現象。

它已被解釋爲（i）一種預形成的有序狀態，隨着相位相干性的逐漸建立，或（ii）兩種競爭相的結果。

目前通過q依賴性出現和消失的類似圓頂的結構，這一結構由相的兩個臨界點的殘餘熵的相對強度控制，爲形成圓頂形相提供了另一種可能性。

AI輔助科學研究，潛力巨大

總而言之，用簡單的話概括就是，一維J_1-J_2 q狀態Potts模型得到了精確解，其中的關鍵在於發現q^2×q^2轉移矩陣的最大特徵值位於一個2×2的最大對稱子空間。

而且維J_1-J_2 q狀態Potts模型被證明與一維q狀態Potts模型等價，其中J_2充當最近鄰（NN）相互作用，J_1充當磁場。

模型的基態被發現包含三個相，這些相由兩個臨界點分開，對於所有q值均如此。

兩個臨界點的殘餘熵的相對強度，隨着q變大而變大。

對於小q和大q出現和消失的類似圓頂的隨機二聚化相，新研究提供了一種新的形成圓頂形相的機制。

而這項研究之所以能完成，都是基於o3-mini-high精確解決了q=3的情況。

這也提示我們，AI提供的廣泛信息中，能給研究者提供充分的洞察和激勵，儘管它的結論可能並不完美。

就在最近，諾獎得主、GoogleDeepMind CEO Demis Hassabis 評論AlphaFold時這樣表示：通過AI，人類現在可以在一年內完成10億年的博士研究時間。

可以想見，未來AI輔助做出的科研突破還將層出不窮。