“DeepSeek许多重要创新出自实习生之手。”

这是前段时间社交网络上盛传的信息，不过这条信息并不夸张，因为辛华剑就是在DeepSeek实习期间主导开发了专注于数学证明DeepSeek-Prover系列模型，他也是DeepSeek-Prover-V1.5论文的一作。

图片来源：DeepSeek-Prover-V1.5论文

辛华剑本科毕业于中山大学逻辑学专业，现在是爱丁堡大学人工智能方向的一年级博士生，专注于大模型在数学定理证明中的创新应用。

去年8月发布的DeepSeek-Prover-V1.5可以被看作是DeepSeek在数学证明领域的早期探索和技术积累，推动了大模型更好地解决形式化定理证明问题，当时被称为是“最强形式化推理模型”。

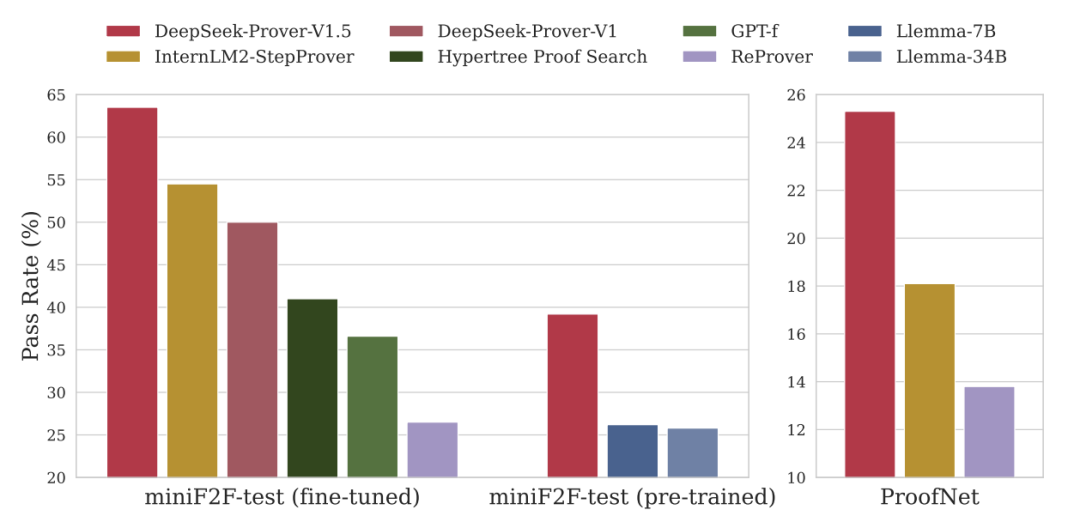
模型在Lean 4形式定理证明基准上的通过率：DeepSeek-Prover-V1.5在高中阶段miniF2F-test基准（Zheng et al., 2022）和本科阶段ProofNet基准（Azerbayev et al., 2023）上表现突出，图片来源：DeepSeek-Prover-V1.5论文

在大模型中，非形式化推理是其理解和生成自然语言、进行常识推理的基础，就像是人类平时聊天或思考问题时的自然方式；而形式化推理则赋予大模型在特定领域（如数学、代码）进行精确、严谨推理的能力，它有严格的规则和格式，每一步推理都必须符合逻辑规则，不能随意跳步或省略。

“DeepSeek-Prover在DeepSeek算是一个比较独立的探索性项目，它的初衷是探索通过形式化系统更好地构造自然语言的严格推理数据。”辛华剑告诉“甲子光年”。

随着AI推理能力的提升，使用AI来证明数学问题已经成为一个重要的研究探索方向，形式化数学也成为了讨论热点。

形式化数学是指使用严格的数学语言和逻辑系统来描述和推理数学概念、定理和证明的过程。著名数学家陶哲轩就认为，形式化数学和AI的结合将使数学研究更加高效、协作和规模化。他乐观地预测，未来数学家可以在AI的辅助下，一次性证明数百或数千条定理。

英国当地时间2月14日下午，在UKTI.HUB（英伦科创）举办的活动上，辛华剑发表了一场题为《大语言模型时代的形式化数学革命》的演讲并回答了“甲子光年”和现场观众的提问。伦敦大学学院（UCL）里的一间教室，涌入了180多名观众。

“这个项目的理想是，最终能够推出一种服务或产品，帮助数学家快速验证一些比较简单的猜想，把数学家从细节当中解放出来。”辛华剑说。

本文，“甲子光年”首家整理呈现辛华剑在本场活动的演讲和问答环节。其中问答在文中最后一部分，辛华剑回答了DeepSeek算力利用率、MCTS对模型训练意义、大模型幻觉、AI未来发展等问题。相关内容经编辑后有删改。

1.形式化数学的历史渊源

大家好，我是辛华剑。

今天我将和大家分享一些关于形式化数学的背景知识，以及探讨如何利用大语言模型在数学推理中应用形式化方法，并展望其可能带来的未来影响。

需要强调的是，接下来我所分享的内容，纯属个人观点，不代表任何组织机构的立场。

首先，什么是形式化数学？

或许对大家来说，这并不是一个非常熟悉的概念。简单来说，形式化数学强调使用精确的符号语言来表达数学陈述和证明，其所有的定理及其证明都必须从一些确定的公理出发，并遵循明确的、可以被机器验证的逻辑规则。

事实上，形式化数学并非一个全新的概念，它有着悠久的历史。

早在莱布尼茨时期，他就提出了“普遍语法”的概念，希望人类所有的思想都可以通过计算来判断真假。比如说当两人发生争执时，只要坐下来计算一下，就能得出谁对谁错的结论。他希望用代数符号的方法来刻画这种操作，这实际上可以看作是现代逻辑学的肇始。

时间来到希尔伯特时代，形式化数学作为一项研究计划已经基本成熟。在他的时代，我们如何进行形式化数学呢？首先，我们需要挑选公理系统，并验证其一致性、相互独立性和逻辑完备性。此外，还需要考虑一个关键问题：是否存在一种能行的方法，能够在一个理论中判定一个问题的答案？虽然哥德尔、丘奇和图灵的工作已经否定了这种可能性，但数学的机械化或自动化仍在不断发展。

从20世纪30年代开始，布尔巴基学派强调使用公理化的方式来重构整个数学体系。他们认为，人类数学家并非无所不能。当他们对某些数学文本的正确性产生质疑时，他们诉诸于将它们进行形式化的一种可能性，直到他们认为这种可能性只是一种练习，不需要额外的思考，他们就会停止这样形式化的过程。

这也就是说，形式化是他们保证数学正确性的一个根本策略。

进入计算机和人工智能时代，麦卡锡提出了使用计算机来书写和检查证明，他认为这样的证明可能会比数学家给出的更短。这是因为许多具体细节可以由计算机来代替人类进行验证，可以被很好地封装起来，不暴露给数学家。数学家只需要关注证明的主要内容和数学思想，一些边界条件之类的检查，就可以完全交给计算机来处理。

2.当代数学的工程化挑战

虽然形式化数学拥有好的历史渊源，为什么它至今仍未被数学界广泛采纳？以及，为什么我们认为它将引发一场革命？

我们认为，当代数学面临着一种工程化的挑战。

我们观察到，现代数学证明的篇幅已经变得极其庞大，动辄数百页甚至上千页。要掌握如此庞大的证明篇幅规模，并通过同行评审进行验证，需要耗费巨大的人力成本。

举个例子，即使人类专家花费数年时间共同验证一个大型证明，仍然有可能出现错误。例如，四色定理的早期证明最初被接受，但后来却被发现存在问题。

此外，知识管理也是一个关键问题。

随着数学的不断发展，无论是在学科分支的数量上，还是在每个学科的深度上，都已经远远超出了一个人类专家能够掌握的范围。

我们会说亨利·庞加莱是最后一位全才数学家，现在已经没有人能够掌握所有数学分支的最新进展。数学家之间在工作上呈现相对分散的状态，这对于数学的可持续发展来说并不是一件好事。

一个典型的例子是，2003年，黑尔斯提出了关于开普勒猜想的一个长达300页的证明。《数学年鉴》（Annals of Mathematics）组织的12人小组花了四年时间，也没有对其正确性做出十足的判断。最终，黑尔斯组织21个人的团队花了12年时间，将这个庞大的数学证明利用Isabelle和HOL Light（证明助手软件，能够保证了证明之于“数学公理”与“逻辑规则”是正确的）上进行了形式化，才最终验证了其正确性。

事实上，黑尔斯在他的原文中提出要做这件事的目的，并不仅仅是为了打消这12人的疑虑。他认为，对于数学的长期发展而言，形式化方法是一个根本的解决方案。

时间来到2024年，陶哲轩也正在推进关于形式化数学方向的研究。

有采访者问陶哲轩：“为什么形式化数学使得数学家互相之间对工作结果的信任有了改变？”陶哲轩说，形式化数学最好的一个特性是，它能够将一个大的问题分解成相互独立的很多方面，大家只要根据自己所专长的方面来提交自己的证明代码，而证明代码的正确性验证是由证明助手以计算机程序执行的方式来彻底完成的。也就是说，数学家不需要逐行检查别人的证明是否真的完全正确，才愿意相信他的工作成果。

因此，他认为这种工作方式是一种更加可以扩展到大规模的数学工作方式。他在对PFR假设的证明进行形式化的项目中，与超过20人的团队来协作完成，这已经比他通常合作的规模要大一些。他认为，随着大家对这套计算机辅助证明系统的了解，以及对这种形式化数学的工作方式的了解，实际上可以推广到更大的规模。也就是说，我们可以像软件工程大规模开发一样来做数学，他认为这是一种非常现代化的方式。

另一方面，爱丁堡大学信息学院的教授Alan Bundy总结道，随着数学的规模越来越大，我们面临一个二难推理：要么我们必须放弃所有这种大定理，要么我们必须诉诸于计算机的辅助来进行证明。

3.形式化数学作为一种解决方案

那么，形式化数学作为一种解决方案，是怎样被实现的？

这里举一些具体的例子。

现在流行的智能助手语言大概有四种，例如Coq、Lean、Isabelle和Mizar。

以Isabelle为例，我们如何在Isabelle中进行形式化证明？一个非常具体的例子，也是在Wikipedia上提供的演示例子：如何证明√2不是一个有理数？

我们会发现，这个在Isabelle中进行的证明在思路上与人类的证明是一致的，它也利用反证法，也逐渐推出一些中间结论，并利用这些中间结论逐步推导出矛盾。

最关键的是，我们不仅仅要在一个定理的证明内部进行工作，我们实际上操作的是一个非常大的数学理论。这个庞大的理论涉及到非常多的定义、引理和定理，我们如何管理它们之间的相互关系？

陶哲轩在他的PFR项目中已经演示了Lean blueprints带来的工作方式变化。其中，绿色的点是已经完成证明的部分，蓝色的点是正在尝试进行证明中的定理，白色的点表示还没有被编写的部分。而图上的点之间的连线描述了这些定义和定理之间的依赖关系，也可以帮助更好地理解和分析整个项目。

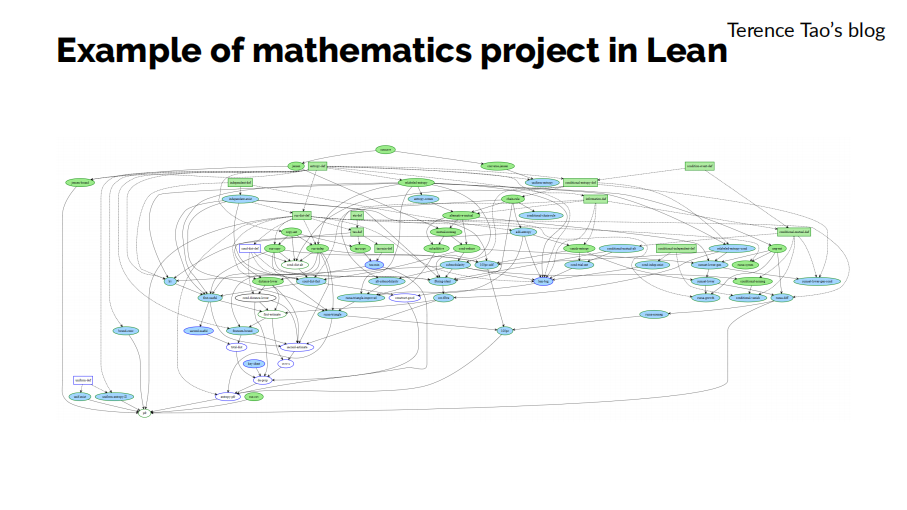
当这个blueprint中所有的点都变成了绿色的时候，我们就可以确凿无疑地判断这个整套数学理论已经完成证明了。

但是，为什么现在大家在学校里仍然使用自然语言来学习和研究呢？这是因为有很多的阻碍，使得我们还没有采用形式化的方法。

一方面是文化上的阻碍。数学工作者仍然更习惯于使用纸笔来进行更灵活的推导，而形式化数学往往只被认为是工程化的辅助技巧，而不是在数学思想上有启发的技术。

另一方面，形式化数学的学习曲线非常陡峭。它有非常复杂的程序语法和语义，需要使用者同时了解数学思想、以类型论或集合论进行形式化的逻辑方法，以及编写程序语言的技术。

结果就是，同样一个证明，在形式化系统里面做和用自然语言做相比，很多时候要多花十倍甚至二十倍的人工成本，这其中包括要额外证明很多在直观上非常直接的、但严格证明非常琐碎的引理。

其他的因素还包括，可能你在Mathematica里面可以顺利地算出一个很复杂的积分，但要使这样的积分结果被Lean这样的严格证明系统接受，目前仍然缺乏自动化的衔接机制。

4.大语言模型在形式化数学的应用

接下来，我想和大家探讨一下大语言模型（LLM）在形式化数学领域的发展。我将从以下几个方面展开：

目前 AI 发展到了什么阶段？

如何将 LLM 应用到形式化数学中去？

LLM 在形式化数学领域未来的发展方向是什么？

面临的挑战和局限有哪些？

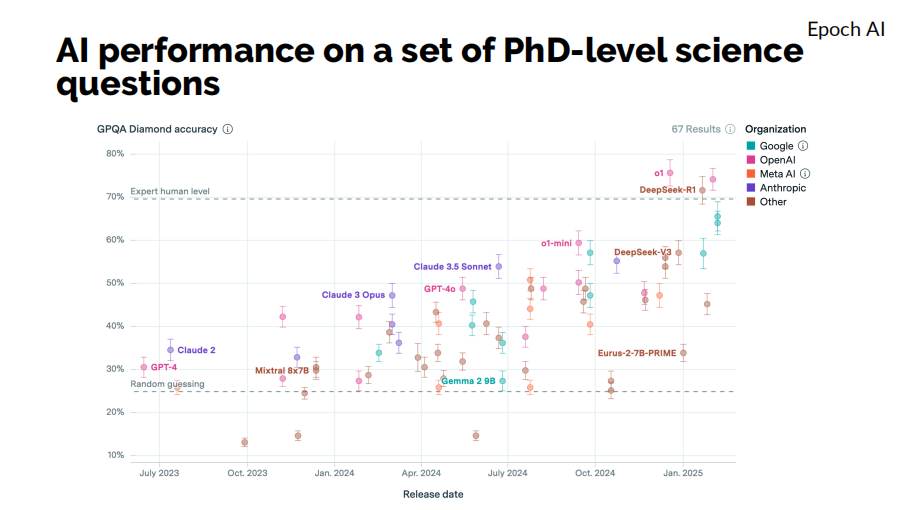
首先，我们可以考虑GPQA Diamond，这是一个衡量PhD水平科学问题的榜单。我们可以看到，从2023年到2025年，大语言模型在解决这些问题上的能力有了显著提升。特别是OpenAI的o1、o3和DeepSeek-R1等模型，其水平已经略高于人类专家的水平。

这意味着，我们距离实现通用人工智能（AGI）可能已经并没有想象中那么遥远。

另外，OpenAI 前不久发布的一份报告显示，目前最先进的大语言模型在算法竞赛上的表现也十分惊艳。在codeforces编程竞赛平台上，o1模型最高能达到98%甚至更高的分位数，这意味着它已经位于前2%的水平。在2024年国际奥林匹克数学竞赛（IOI）上，他们的模型能达到362分，这已经达到了人类金牌选手的水平。

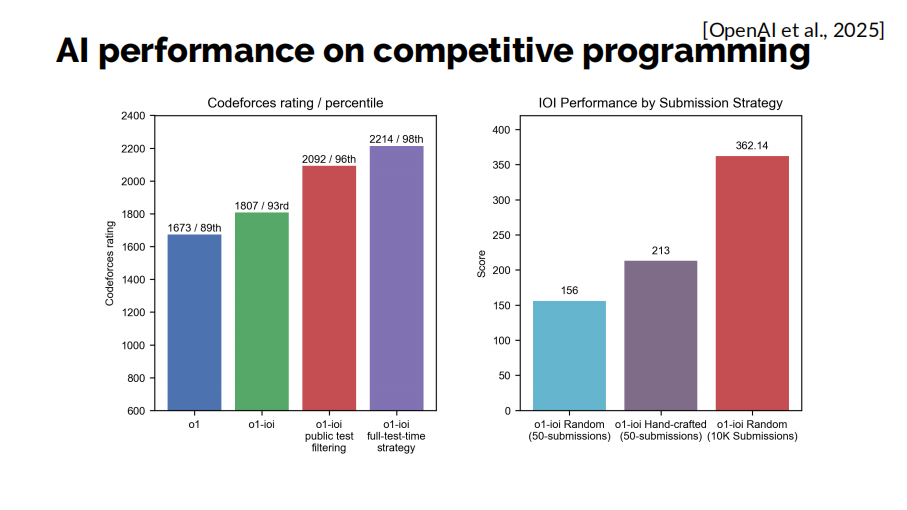
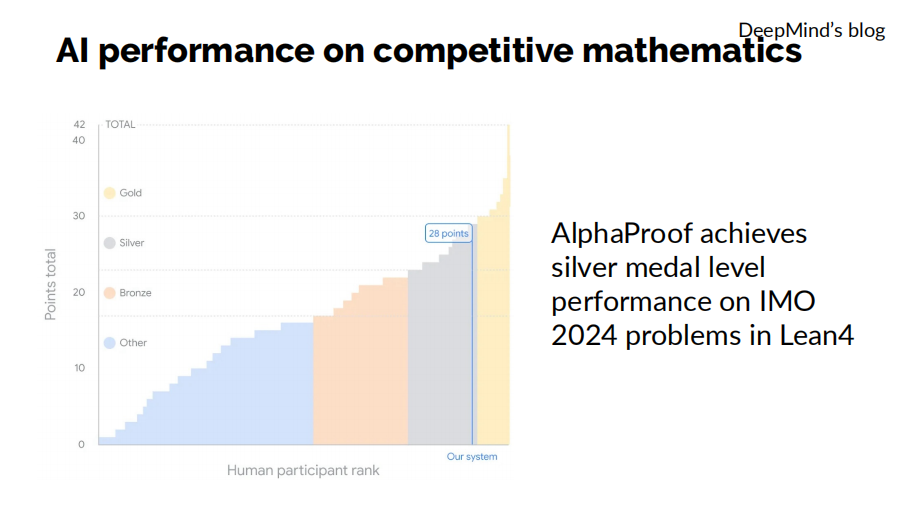
在数学方面，DeepMind去年7月份发布的形式化数学定理证明模型AlphaProof也取得了重要进展。和我们的做法一样，该模型也不是在自然语言上进行训练和测试，而是在形式化证明系统Lean中进行的。它与专注几何的模型AlphaGeometry2一道，在2024年的国际数学奥林匹克竞赛（IMO）中获得了28分的成绩，距离金牌水平仅差1分。

那么，这些看起来像是奇迹的模型是如何训练出来的呢？其背后的训练机制是怎样的呢？

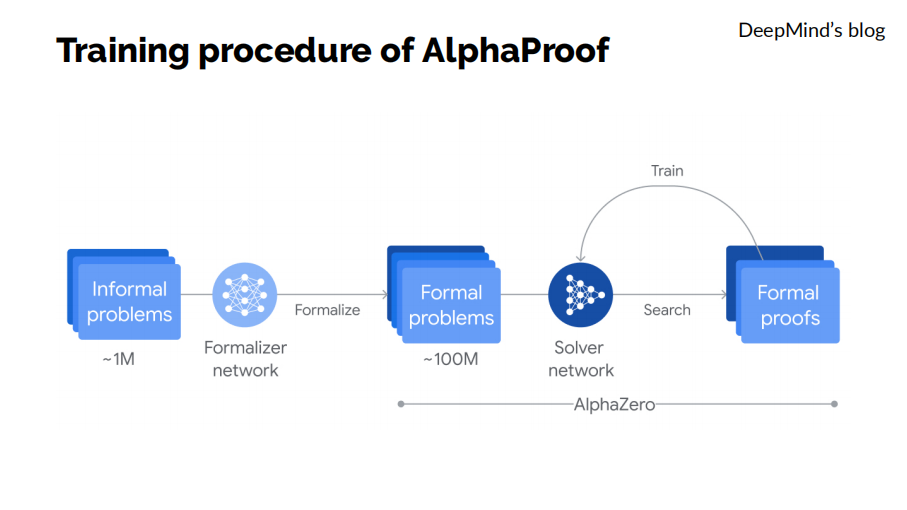
以AlphaProof为例，它的训练流程大致分为两部分。第一部分先收集 100 万道人类数学问题，这些问题以自然语言描述，再使用神经网络将其翻译成一亿道形式化数学问题。

然后，我们在此基础上训练解题神经网络。该网络采用了类似于AlphaGo的强化学习方法，不断地尝试对数学题目搜索证明，成功通过形式化验证的证明拿来进行训练，以此不断迭代，不断提升解题神经网络的性能。

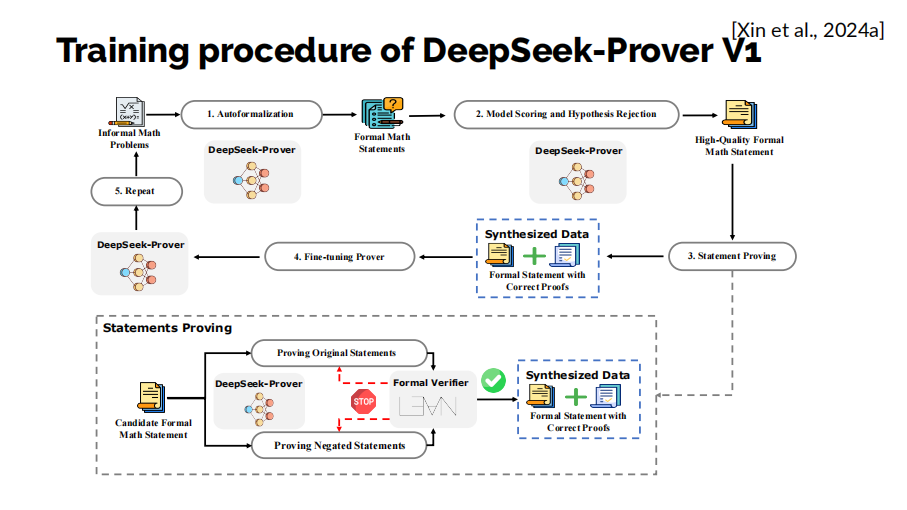
事实上，在2024年5月，我们的DeepSeek-Prover团队就已经提出了一个相似的方法：我们同样通过大规模的自动形式化方法来合成证明数据，进行迭代训练，不断提升定理证明模型的表现。

在我们的论文中，还分享了一些数据合成流程设计的细节。例如，使用模型生成的形式化数学问题可能是错误的，我们就让模型同时尝试证明它和证伪它。类似于AlphaGo在围棋中进行“左右互搏”的方法，只要有一方面的证明成功，我们就认为模型成功证明了该定理，并把该证明加入训练数据中继续进行迭代。

MiniF2F是一个标准的形式化定理证明Benchmark，主要衡量模型在高中数学竞赛中的表现。2024年5月，我们的DeepSeek-Prover V1模型打破了Meta维持了两年的SOTA（最先进水平）。此后，该领域变得越来越活跃，各种方法层出不穷，形式化定理证明模型也以更快的速度发展。

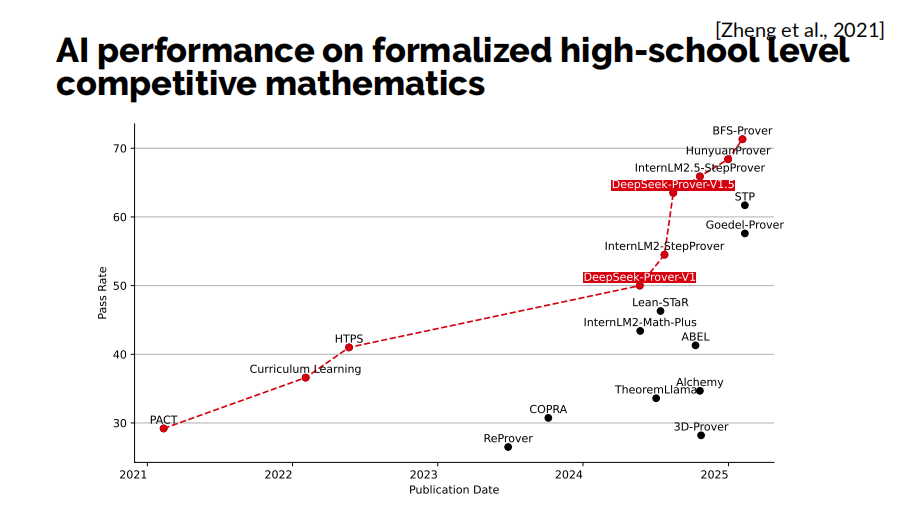
值得一提的是，在我们于2024年8月推出的DeepSeek-Prover-V1.5中，已经训练得到了一些与目前流行的推理模型相似的行为模式：大模型先进行一系列的思维步骤，然后再将这些思维步骤转落实为正式的回答。

正如以下实例展示的那样，模型首先在注释块中进行完整的推理再开始进行形式化编码，甚至在正式代码的写作中，对每一行证明的写作前都先进行思考和规划。这表明，我们的模型在一定程度上已经具备了先思考再作答的能力。尽管它在反思和回溯能力上仍然与目前最先进的推理模型有距离，但我相信这或许将是形式化数学定理证明模型的下一个突破的方向。

通过这个例子，我希望表达的是：形式化数学作为大语言模型的一个应用领域或一种实践方向，为探索模型推理能力的训练提供了严格验证反馈的良好环境，能够在一定程度上对其他更通用领域的研究起到借鉴作用。

接下来，我想谈谈对未来发展方向的展望。在形式化数学定理证明的领域，我们期望使用大语言模型在哪些方面取得进一步的突破？

首先，我们希望语言模型能够主动提出一些有意义的数学猜想，证明它们可以帮助我们更好地完成目标定理的证明，或者发现已有数学结论之间的深层联系，甚至指导未来的数学研究方向。

更进一步，我们希望模型能够独立的发现一些数学抽象。

事实上，数学研究中最好的工作是能够发现一些独创的结构，而往往不仅仅是解决已经提出的猜想，也就是我们所熟悉的一句话就叫“提出问题比发现问题更重要”。

比如巴拿赫就说过，好的数学家就是发现定理之间、定理的证明之间的相似性，而最好的数学家能够发现类比之间的类比，或者说发现更加高阶的抽象。

这方面的工作其实也已经有探索，比如说在2021年时候有一个叫DreamCoder的项目，已经在相对简单的Lambda Calculus上取得了进展。它从一些非常简单的概念出发，能够成功抽象得到复杂的概念，甚至发现了一些物理定律。

最后， 我们希望语言模型能够独立地构建一个完整的数学知识库。

例如，人类在数学工作中、甚至是模型在迭代训练中都会发现很多零散的定义和结论，它们之间存在重叠或依赖关系。我们希望语言模型能够以一种结构化的方式将它们整合起来，形成一个层次分明、结构良好的知识体系，在其中更一般的定理可以统摄更具体的定理，实现从高层观点到初等事实之间的整合。

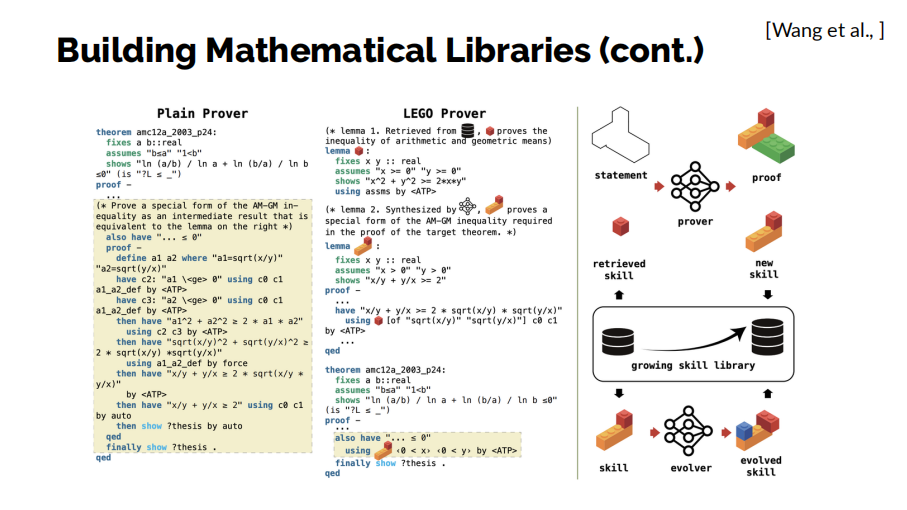
实际上，我们在2024年也已经有一个非常相似的工作，LEGO Prover，它获得了2024年顶级学术会议ICLR的口头报告推荐。和以往的的模型尝试直接生成完整证明不同，我们让模型在尝试证明之前先提出一些引理，利用这些引理能够帮助我们更好地证明目标定理。在这个过程中得到的这些引理会被收集到技能库中以供稍后复用，以这种方式我们能够引导模型积累知识、提升性能。模型手上的工具越来越多，可以更好地来适应由弱到强的泛化，一步一步地学会做一些更加复杂的问题。

5.LLM在形式化数学中的挑战和局限

最后想要分享一下在形式化数学定理证明领域应用大语言模型仍然存在的一些挑战和局限。

首先，数据稀缺。大语言模型的训练是超大规模数据驱动的，但形式化数学领域的数据相对稀缺。这使得直接训练模型变得非常困难。因此，这个领域的发展会更加依赖合成数据的作用。

其次，自然语言与形式语言的翻译。正如我们之前谈到，自然语言和形式语言之间的相互翻译并非易事。

第三，形式系统的复杂性。形式系统为了保证严格推理，每个定理都必须在原则上能够追溯到原始公理，这会导致整个系统变得非常臃肿庞大。例如Lean的标准数学库中有超过2000个代码文件、将近180万行代码，进行新的定理证明需要准确调用其中已有的结论，这实际上是一个非常困难的任务。我认为要使用大语言模型做好形式化数学需要拥有在大规模代码库上工作的Agent能力，而这目前是一个公认的挑战。

那么，如果我们在数学领域成功应用了大型语言模型，又意味着什么呢？

我会从对数学研究、对工业规模的验证、对数学教育、对一般应用这四个方面去谈。从我个人的观点看，DeepSeek之所以受到这么大的关注，很大程度上是因为它展示了一个道理：如果说智能可以就像自来水一样，价格低廉、规模可扩展、质量可以信赖，它是会改变整个世界的。这就像古罗马能够创造一种繁荣的文明形态，与输水管道等可靠的基础设施是密不可分的。

对于数学研究而言，我们希望能开发一种服务或产品，帮助数学家快速验证一些简单的但劳动密集的猜想，将他们从繁琐的细节中解放出来。语言模型可以充当人机交互的接口，将自然语言问题翻译成代码，利用已有知识库中进行严格验证，并将结果以自然语言的形式反馈给数学家。

第二个方面就是关于工业中的大规模验证。事实上，除了数学之外，形式化方法也在软硬件验证上有广阔的应用，例如英特尔在芯片验证上广泛使用了大规模的SAT/SMT求解器，而定理证明器可以在更高层次的抽象上完成严格的规约验证。然而，由于需要专家花费长时间进行证明编码，在实践中广泛实施中的代价非常高昂，极大限制了形式化方法的应用。我们希望语言模型能够加速形式验证的普及，使其能够以更低廉、更可扩展的方式应用于更广泛的领域，避免软硬件漏洞可能导致的巨大损失。

第三个方面就是教育。我们可以保存和传承那些可能被遗忘的数学知识。随着老一代数学家的退出，他们的研究成果可能会逐渐被人遗忘。但语言模型可以成为一种可扩展的知识载体，保存和传承这些长尾的数学知识。

最后，对于一般的应用来说，实际上数学并不只是数学家关心的问题，在生活、工作中有很多事情可以用数学的办法解决。一个例子是运筹优化，目前的解决方案也因为专家人工成本过高而无法惠及所有需求，但大语言模型可以大大降低成本、扩展适用的规模。另一个例子是算法开发，构想一个算法往往是比较快速的，但是我们如何能够判断这个算法的效率？这实际上是一个比较复杂的数学问题。如果说我们有一个非常好的数学大语言模型，能够帮我们快速运用数学工具估计一些复杂算法的复杂度的话，那这对算法的演进也是一件好事。

总之，大语言模型为数学提供了一种严格且可持续的知识载体和应用手段，我们认为它在自动化形式化和定理证明方面具有广阔的应用前景。

虽然目前仍然面临数据稀缺、自然语言对齐以及系统复杂性等挑战，但我们相信，随着技术的不断发展，大语言模型将在数学领域发挥越来越重要的作用，同时也将推动软硬件验证以及其他科学应用的进步。

6.问答环节

问：DeepSeek有哪些创新之处？这些创新对AI开发者有哪些启示？在提升算力利用率方面，我们应该关注什么呢？

辛华剑：DeepSeek震动华尔街一个方面是它的训练成本非常低，这与DeepSeek在算力管控方面的工作密不可分。在实际工作中，尤其对于大模型而言，如何制定合适的算力策略至关重要。如果我们有更多的卡，肯定不会太顾及算力的使用效率，所以有些时候资源有限是能够促进创新的活跃的，但另一方面，在算力不足的情况下，也难以在scaling law上获得正确的认知。这其实是一个比较矛盾的问题。

问：DeepSeek-Prover-1.5的定理证明在逻辑上是百分之百正确的吗？

辛华剑：我们强调通过验证的证明是正确的，但这句话的前提在于我们对数学问题进行的形式化建模是正确的，以及它所最终实现的这个程序语义是符合我们期望的。

问：MCTS（蒙特卡洛树搜索）对于模型训练很重要吗？

辛华剑：我们在DeepSeek-Prover-V1.5阶段确实做了MCTS，但我们发现MCTS和独立的采样相比，表现并没有非常大的收益。这可能与DeepSeek-R1技术报告里说MCTS不太成功的结论是吻合的，不过在做R1的时候我已经离开DeepSeek了，所以我也只是猜测。

问：在资源有限的情况下，如何分配训练和推理资源才能达到最佳效果？“大模型+无推理”和“中模型+花费更多token来做推理”哪个更好？

辛华剑：这是一个非常好的问题，也是我们在做Prover项目中实际面临的挑战。比如，在初期探索阶段，我们是用小规模模型（如几百M）进行大规模的MCTS（蒙特卡洛树搜索），还是用更大规模的模型（如几十B）来做小规模的推理？一个可以参考的例子是，去年在AIMO（人工智能数学奥林匹克竞赛）的第二名团队对模型采样方法以及规模上的平衡做了细致的研究，大家参考他们的报告《An Empirical Analysis of Compute-Optimal Inference for Problem-Solving with Language Models》。

问：AI是否会取代人类从事科研工作？例如，在数学、物理、化学等领域，哪些学科更容易被AI赋能？

辛华剑：我个人从事AI For Math的研究，我认为数学是一个AI与人类进行沟通的良好桥梁。因为数学是一个更倾向于纯粹的思辨，而非实验的学科。这使得在AI大模型开发阶段，与环境交互的方式更加简洁，从而方便AI算法的开发和验证。当然，最近我们也看到AI在实验科学领域也有所应用。例如，有研究机构尝试让AI参与实验，甚至让AI像学生一样手动进行实验，从中获取经验和知识。我认为，AI在各个科研领域都在进行探索，而未来2到5年可能会有更显著的进展。

问：LLM的幻觉问题会对数学定理造成怎样的影响？

辛华剑：这个问题非常困扰我们。我们发现很多时候它会提出一些数学库里面根本就没有的定义或定理，或者说它在训练过程中记住了一些名字，但这些名字在当前的使用阶段已经不再使用了，但模型仍然会使用类似的东西。我觉得这方面的解决归根结底需要Agent能力，需要大语言模型和整个系统进行充分的交互，实际判断它现在工作的这个基础数学库到底已经有什么样的内容。

问：展望未来十年，人工智能领域最令人兴奋的机会是什么？最大的挑战又是什么呢？

辛华剑：事实上，在o1出现之前，我根本没有想到可以把思维链拉得这样长，出现足够自主反思能力的推理模型。我认为这样的技术进展，往往非常跨越性的，即使是在一线训练模型的同学也不一定能对未来有准确的预测。我感觉很多时候AI就像一种魔法，它会有怎样的结果，只有真正动手试一试才知道。对于我们来说这恰恰是做AI研究工作最大的motivation（驱动力），它确实是一个需要充分想象力的学科。