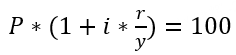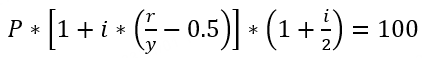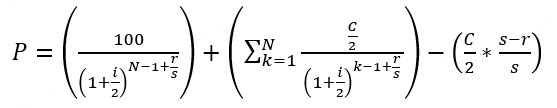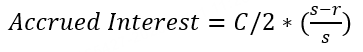国债交易的名词解释
国债信息 | 解释 |
债券价格 | 债券价格就是您买入这张债券的价格,这个数据在交易时间内可能随时变动。 |
到期年化收益率 Yield to Maturity,YTM | 指投资者持有债券至到期日、并假定债券本金和利息都按时支付时,投资者将获得的年化回报率(未考虑交易佣金成本)。 按到期收益率对债券所有未来的现金流进行折现,所得到的现值和买入价格相等,即未来得到的利息支付和最终本金偿还的现值总和,等于债券当前的市场价格。
|
派息频率 | 派息频率是指这张国债一般会按照怎样的时间频率进行派息,比如一年两次或者一年一次。美国国债notes和bonds都是一年约定两次派息。 |
剩余期限 | 剩余期限是从现在买入至该国债到期,还剩余多少年限。 |
到期日 | 是指国债的到期时间。 |
执行日 | 交易达成的日期,但还未发生债券所有权的转移 |
结算日 | 交易最终完成的日期,买方必须向卖方付款,同时卖方将资产交付给卖方。为执行日后一天。应计利息的计算以结算日为准。 |
买入参考价 | 买入参考价(Bid Price),指从平台处买入债券的参考价格,T-Bill的报价通常为利率,即Discount Rate;Bond和Note的报价通常为价格。报价不含交易佣金和应计利息。 |
卖出参考价 | 卖出参考价(Ask Price),指把自己持有的债券卖出时,买方支付的参考价格。 |
中间价 | 是指市场上的买入价格和卖出价格之间的中间点。您可以使用中间价作为参考,因为它通常反映了市场上的供需情况。 |
久期 | 久期(Duration)是一个用于衡量债券价格对利率变化的敏感度指标,它可以帮助您预测债券价格在市场利率上升或下降时的变化方向和幅度。 |
修正久期 | 修正久期(Modified Duration)是久期的变种,通常用于衡量债券价格对利率变化的绝对变化幅度。 |
凸性 | 债券的凸性(Convexity)是一个金融指标,用于衡量债券价格对利率变化的非线性响应。凸性是债券的价格与其预期收益之间的二阶导数,它考虑了当市场利率发生变化时,债券价格的曲线弯曲程度。 |
应计利息 | 应计利息不是费用,而是买家支付给卖家的持有期间的利息,虽然债券一般是半年才派息一次,但是买入持有之后每天都会计算应计利息,交易时买家需要支付这部分钱给卖家。应计利息会在派息之后清空并重新计算。 其中,C=票息,s = 当前付息期总天数,r = 当前付息期剩余天数 举个例子来说明应计利息:2021/12/18发行的5年期note,票息 = 5,到期日为2026/12/18。当前结算日为2023/10/31,下一付息日期为2023/12/18,上一付息日期为2023/06/18. 故:s = 下一付息日 - 上一付息日 = 2023/12/18 - 2023/06/18 = 183天 r = 下一付息日 - 结算日 = 2023/12/18 - 2023/10/31 = 48天 Accrued Interest = 5/2 * (183 - 48) / 183 = 1.84426 暂时无法在飞书文档外展示此内容 註:执行日(Execution Date)是交易达成的日期,但还未发生债券所有权的转移 结算日(Settlement Date)是交易最终完成的日期,买方必须向卖方付款,同时卖方将资产交付给卖方。为执行日后一天。 应计利息的计算以结算日为准。 具体的天数根据当期实际天数计算。Bonds and notes issued by the U.S. Treasury earn interest calculated on an actual/actual basis. 所以,如果您在 10 月 31 日购买了这张国债,您需要支付给卖家大约 1.84 美元的应计利息,以补偿他应该获得的利息。然后,在当年的 12 月 18 日,您将获得全部利息支付。 (註意:以上案例为方便理解,採用应计利息的通用算法,每个机构对于“计息繫数”定义不同,需要以实际计算结果为准) |
债券或票据的价格是如何决定的?
债券或票据的价格可能是面值(也称为票面价值),也可能高于或低于面值。价格取决于到期收益率和票息。
如果YTM到期收益率 | 债券/票据的价格会 |
高于票息 | 低于面值 |
等于票息 | 面值 |
低于票息 | 高于面值 |